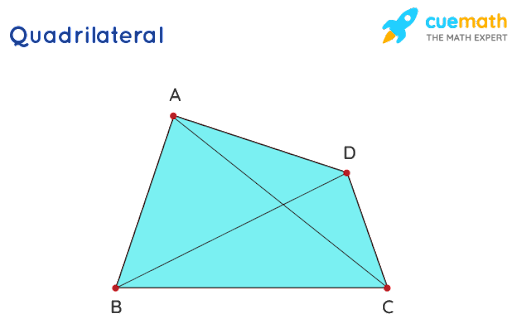
Definition If we have four non colinear, we obtain a closed figure with four sides. Such a figure formed by joining four points in an order is called a quadrilateral.
Property of quadrilateral
(1)A quadrilateral has four sides, four angles and four vertices.in short A foure sided figure
(2)A polygon that has four sides, such as a ractangle or rhombus
(3)Also called, tetragon a polygon having four sides. A complete quadrilateral consists of four lines and their six points of intersection.
(4)A quadrilateral has four sides, four angles and four vertices.
Angle sum Property of a Quadrilateral
The sum of the angles of a quadrilateral is 360°.
In above Angle A +Angle B +Angle C +Angle D=360°
Types Of Quadrilateral
(1) Trapezium :IfOne pair of opposite sides of quadrilateral are parallel. Then figure formed is called trapezium
(2)
.(2)Parallelogram : If Both pairs of opposite sides of quadrilateral are parallel. Such quadrilateral are called parallelograms
(B)Square:All sides are equal. All angles are equal and measure 90°
Competencey based Questions
Q(1) Can you give example of squres from your surrounding?
(C)Ractangle :Opposite sides are parallel. Opposite sides are equal. All angles are equal and measure 90°.(D)Rhombus :All sides are equal, opposite angles are equal.
Quadrilateral is a 4 sided polygon bounded by 4 finite line segments. A quadrilateral has 2 diagonals based on which it can be classified in to concave or convex quadrilateral. In case of convex quadrilaterals, diagonals always lie inside the boundary of polygon.
Based on the lengths of sides and angles, common convex quadrilateral are
(1)Trapezoid
(2)Parallelogram
(3)Square
(4)Rectangle
(5)Rhombus
(6)kite
Properties Of Quadrilaterals
(1)Properties of parallelogram
(a)Opposite sides are parallel and equal to each other.
(b)opposite angles are equal
(c)Diagonals bisect each other
(d)Diagonals divide the paralleogram into two congruent triangles
(e)if any one of the angles is 90°,then all angles are right angles
Activity
Cut a parallelogram from a sheet of paper and cut it along a diagonal.
What you find
(a)We find two triangles
(b)when we place one triangle over another. We find that they overlap and are congruent.
(c)Diagonal divides the parallelogram into two congruent triangles.





 Name of the quadrilateral and properties
Name of the quadrilateral and properties 









No comments:
Post a Comment
thank you